跳表(SkipList)
对于一个有序链表,要想在其中查找某个值,我们需要从头到尾遍历链表,这样查找效率就会很低,时间复杂度高,是O(n)。为了提高查询效率,我们在链表之上建立多层索引。每隔几个结点向上抽取一层,建立索引层。提高效率。这种链表加多级索引的结构,就是跳表。可以支持快速的插入、删除、查找操作。数据结构如下图所示。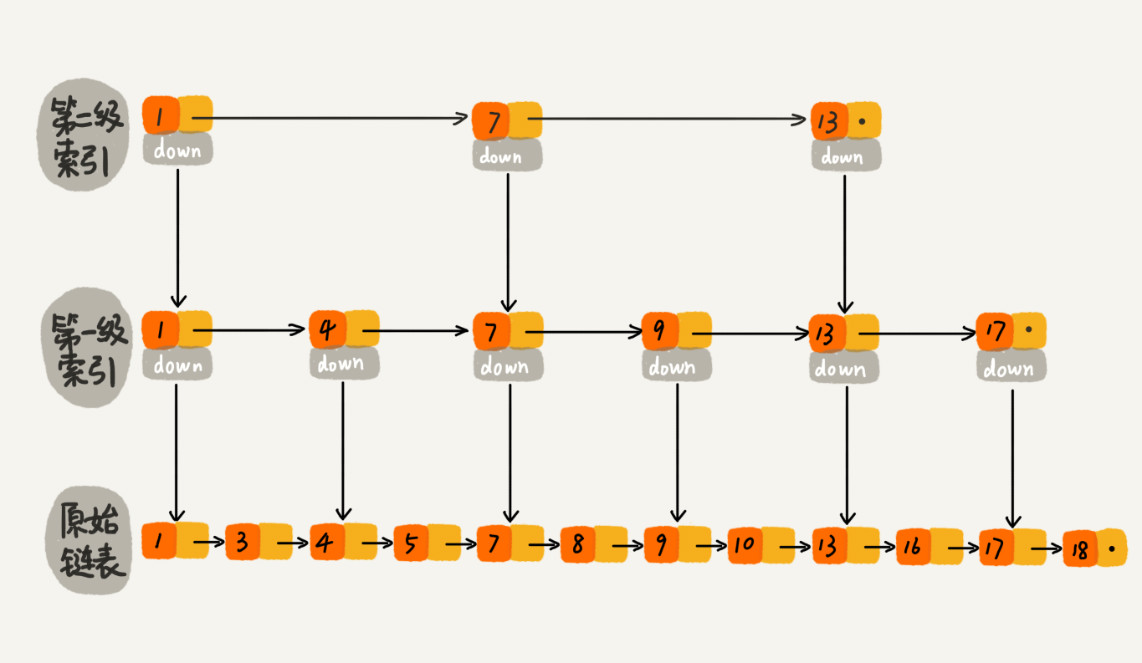
时间复杂度
- 查找时间复杂度:在跳表中查找数据时,首先在最高层索引中查找,缩小查找范围,再向下级索引查找,依次类推,直到找到要查询的数据。假设数据规模为 n,每隔 m 个结点构建索引,最高级的索引有 m 个结点,索引共有 h 级 。可以得到 n / mh = m,从而求得 h = logmn - 1。如果包含原始链表这一层,整个跳表的高度就是 logmn。我们在跳表中查询某个数据时,如果每层都要遍历 m 个 结点,则查询的时间复杂度就是 O(m * logmn)。省去常量则为 O(logn)。
- 插入、删除时间复杂度:链表中插入、删除的时间复杂度都为O(1),但每次插入、删除我们都需要查找数据结点,所以插入、删除的时间复杂度也为O(logn)。
空间复杂度
- 空间复杂度:比起单纯的单链表,跳表需要存储多级索引,消耗更多的存储空间。假设原始链表大小为 n,每 2 个结点建立索引。那第一级索引大约有 n/2 个结点,第二级大约有 n/4 个结点,以此类推,每上升一级就减少一半,直到剩下两个结点。把每层索引的结点数加起来就是一个等比数列。
n/2 + n/4 + n/ 8 + … + 8 + 4 + 2 = n - 2。即需要额外再用接近 n 个结点的存储空间来存储索引。所以跳表的空间复杂度是 O(n)。
以上是每两个结点抽取一个结点建立索引层,也可以每 3 个 或 5 个抽取一个结点。这样可以大幅减少索引层结点占据的空间。但空间复杂度依然是 O(n)。
跳表索引动态更新
当不停的往跳表中插入数据时,如果不更新索引,就有可能出现某两个索引结点之间数据非常多的情况,极端情况下,跳表还会退化成单链表。因此,作为一种动态数据结构,我们需要某种手段来维护索引与原始链表大小之间的平衡。避免复杂度退化,以及查找、插入、删除操作性能下降。
跳表通过随机函数来维护它的平衡性。当我们往跳表中插入数据的时候,我们可以可以选择同时将这个数据插入到部分索引层中。我们通过一个随机函数,来决定将这个结点插入到哪几级索引中,比如随机函数生成了值 K,那就将这个结点添加到第一级到第 K 级这 K 级索引中。随机函数要能够保证跳表的索引大小和数据大小平衡性,不至于性能过度退化。
详细了解跳表这种数据结构,推荐这篇文章。点击这里。
散列表(HashTable)
散列表也叫“哈希表”或“Hash 表”,是根据关键码值(Key value)而直接进行访问的数据结构。它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。散列表用的是数组支持按照下标随机访问数据,时间复杂度为 O(1)的特性,将关键码值(key)通过散列函数(或“Hash函数”、“哈希函数”)映射为数组的下标,将数据存储在该下标对应的位置。散列函数计算得到值叫散列值(或“Hash值”、“哈希值”)。
散列函数
散列函数在散列表中起着非常关键的作用。通常把它定义成 hash(key),其中 key 表示元素的键值,hash(key) 的值表示经过散列函数计算得到的散列值。
散列函数设计的基本要求:
- 散列函数计算得到的散列值是一个非负整数。
- 如果 key1 == key2,那么 hash(key1) == hash(key2)。
- 如果 key1 != key2,那么 hash(key1) != hash(key2)。
针对第三点,看起来合情合理,但是在真实的情况下,要想实现一个不同的 key 对应的散列值都不一样的散列函数几乎是不可能的。因为 key 的可能性是无限的,而通过散列函数得到的散列值却是有限的。所以再好的哈希算法,也无法避免这种情况。我们把这种 key1 != key2,而 hash(key1) == hash(key2) 的情况叫做散列冲突(或“哈希碰撞”)。
散列冲突
再好的散列函数也无法避免散列冲突。常用的散列冲突解决方法有两类,开放寻址法(open addressing)和链表法(chaining)。
开放寻址法
开放寻址法的核心思想是,如果出现了散列冲突,就重新探测一个空闲位置,将其插入。
- 线性探测(Linear Probing)
- 当往散列表中插入数据时,如果某个数据经过散列函数散列之后,存储位置已经被占用了,就从当前位置开始,依次往后查找,看是否有空闲位置,遍历到尾部都没有找到空闲的位置,则再从表头开始找,直到找到为止。
- 当在散列表中查找数据时,通过散列函数求出要查找元素的键值对应的散列值,然后比较数组中下标为散列值的元素和要查找的元素。如果相等,则说明就是我们要找的元素;否则就顺序往后依次查找。如果遍历到数组中的空闲位置,还没有找到,就说明要查找的元素并没有在散列表中。
- 当在散列表中删除数据时,不能单纯地把要删除的元素设置为空,因为在上述查找方法中,通过线性探测方法,在找到一个空闲位置时,就认定散列表中不存在这个数据。但是,如果这个空闲位置是后来删除的,就会导致原来的查找算法失效。因此,可以将删除的元素,特殊标记为 deleted。当线性探测查找的时候,遇到标记为 deleted 的空间,并不是停下来,而是继续往下探测。
二次探测(Quadratic probing)
二次探测,跟线性探测很像,线性探测每次探测的步长是 1,那它探测的下标序列就是 hash(key) + 0,hash(key) + 1,hash(key) + 2 …… 。而二次探测探测的步长就变成了原来的“二次方”,也就是说,它探测的下标序列就是 hash(key) + 0,hash(key) + 12,hash(key)+22……。双重散列(Double hashing)
双重散列,意思就是不仅要使用一个散列函数。而是使用一组散列函数 hash1(key),hash2(key),hash3(key) …… 我们先用第一个散列函数,如果计算得到的存储位置已经被占用,再用第二个散列函数,依次类推,直到找到空闲的存储位置。
链表法
链表法是一种更加常用的散列冲突解决办法,相比开放寻址法,它要简单很多。在散列表中,数组的每个存储位置我们称之为“桶(bucket)”或者“槽(slot)”,它会对应一条链表,所有散列值相同的元素我们都放到相同槽位对应的链表中。当插入的时候,我们只需要通过散列函数计算出对应的散列槽位,将其插入到对应链表中即可,所以插入的时间复杂度是 O(1)。当查找、删除一个元素时,我们同样通过散列函数计算出对应的槽,然后遍历链表查找或者删除。
开放寻址法 VS 链表法
- 开放寻址法
- 优点:开放寻址法实现的散列表中的数据都存储在数组中,可以有效地利用 CPU 缓存加快查询速度。而且,序列化起来比较简单。
- 缺点:开发寻址法实现的散列表,删除数据的时候比较麻烦,需要特殊标记已经删除掉的数据。而且数据都存储在一个数组中,比起链表法,冲突的代价更高。所以,装载因子的上限不能太大且只能小于 1。
- 链表法
- 优点:链表法对内存的利用率比开放寻址法要高。因为链表结点可以在需要的时候再创建,并不需要像开放寻址法那样事先申请好。对大装载因子的容忍度更高。只要散列函数的值随机均匀,即便装载因子变成 10,比起顺序查找还是快很多。支持更多的优化策略,比如用红黑树代替链表。
- 缺点:链表法包含指针,序列化起来就没那么容易。对于比较小的对象的存储,因为要存储指针,是比较消耗内存的,还有可能会让内存的消耗翻倍。而且,因为链表中的结点是零散分布在内存中的,不是连续的,所以对 CPU 缓存是不友好的。
总结:当数据量比较小、装载因子小的时候,适合采用开放寻址法。存储大对象、大数据量的散列表更适合链表法。
装载因子
装载因子(load factor):当散列表中空闲位置不多的时候,散列冲突的概率就会大大提高。为了尽可能保证散列表的操作效率,一般情况下,我们会尽可能保证散列表中有一定比例的空闲槽位。装载因子就用来表示空位的多少。
计算公式:散列表的装载因子 = 填入表中的元素个数 / 散列表的长度
装载因子越大,说明空闲位置越少,冲突越多,散列表的性能会下降。当散列表的装载因子超过某个阈值时,就需要进行扩容。装载因子阈值需要选择得当。如果太大,会导致冲突过多;如果太小,会导致内存浪费严重。装载因子阈值的设置要权衡时间、空间复杂度。如果内存空间不紧张,对执行效率要求很高,可以降低装载因子的阈值;相反,如果内存空间紧张,对执行效率要求又不高,可以增加装载因子的值。
树
树是一种非线性数据结构。如下图所示: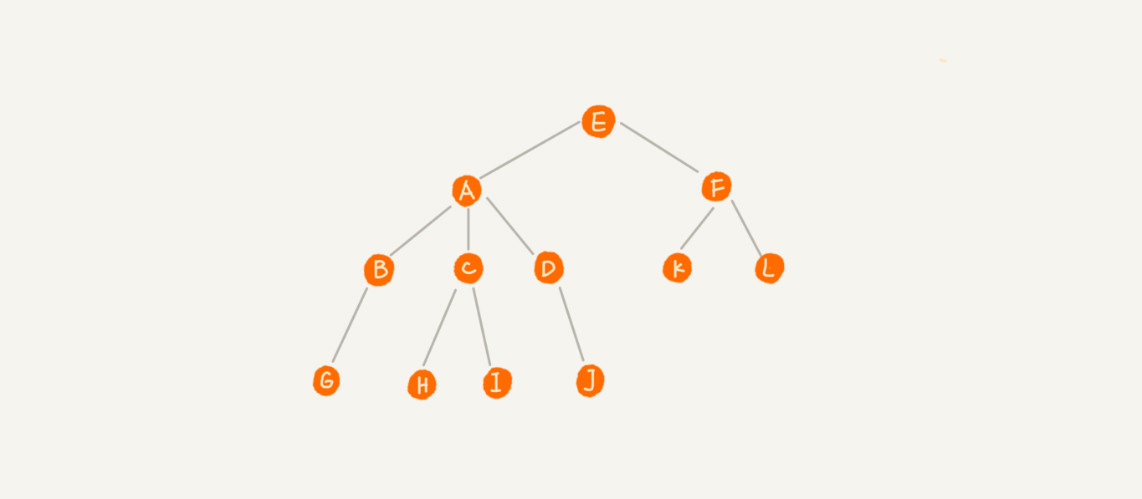
这里面每个元素称为“节点”,用来连接相邻节点之间的关系,我们叫做“父子节点”。上图中,A 节点就是 B 节点的父节点,B 节点是 A 节点的子节点。B、C、D 这三个节点的父节点是同一个节点,所以它们之间互称为兄弟节点。我们把没有父节点的节点叫做根节点,也就是图中的节点 E。我们把没有子节点的节点叫做叶子节点或者叶节点,比如图中的 G、H、I、J、K、L 都是叶子节点。
三个相似概念: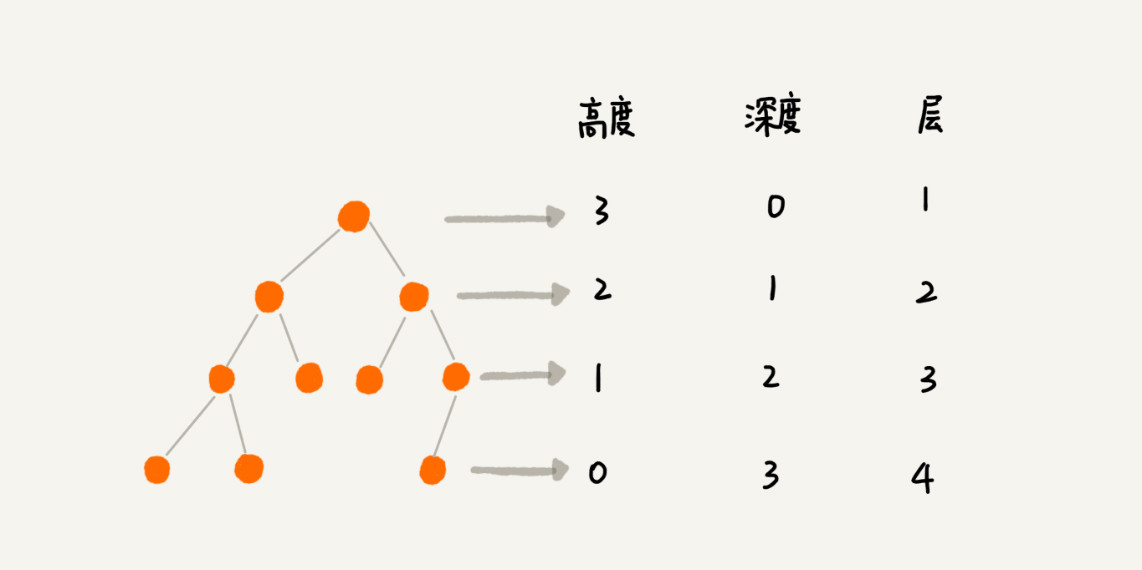
- 高度(Height):节点到叶子节点的最长路径(边数)。
- 深度(Depth):根节点到这个节点所经历的边的个数。
- 层数(Level):节点的深度 + 1。
二叉树
二叉树是最常用的一种树结构,二叉树每个节点最多只有两个节点,分别是左子节点和右子节点。
- 满二叉树:叶子节点全部都在最底层,除了叶子节点之外,每个节点都有左右两个子节点。
- 完全二叉树:叶子节点都在最底下两层,最后一层叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大。
二叉树的存储
- 链式存储法:基于链表存储,每个节点除存储本身数据以外,还有两个指向左右子节点的指针。只要拎住根节点,就可以通过左右子节点的指针,把整棵树都串起来。这种存储方式我们比较常用。大部分二叉树代码都是通过这种结构来实现的。
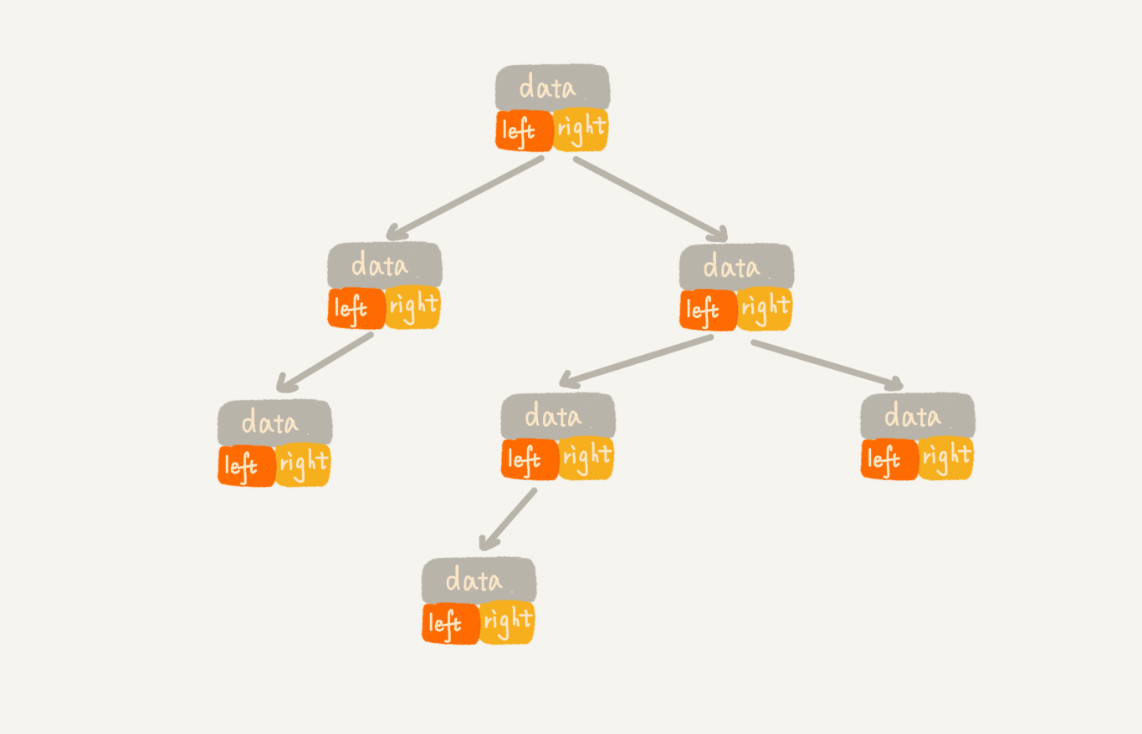
- 顺序存储法:基于数组存储,如果节点 X 存储在数组中下标为 i 的位置,下标为 2 i 的位置存储的就是左子节点,下标为 2 i + 1 的位置存储的就是右子节点。反过来,下标为 i/2 的位置存储就是它的父节点。通过这种方式,我们只要知道根节点存储的位置(一般情况下,为了方便计算子节点,根节点会存储在下标为 1 的位置),这样就可以通过下标计算,把整棵树都串起来。适合存储完全二叉树,如果是非完全二叉树,会浪费比较多的数组存储空间。
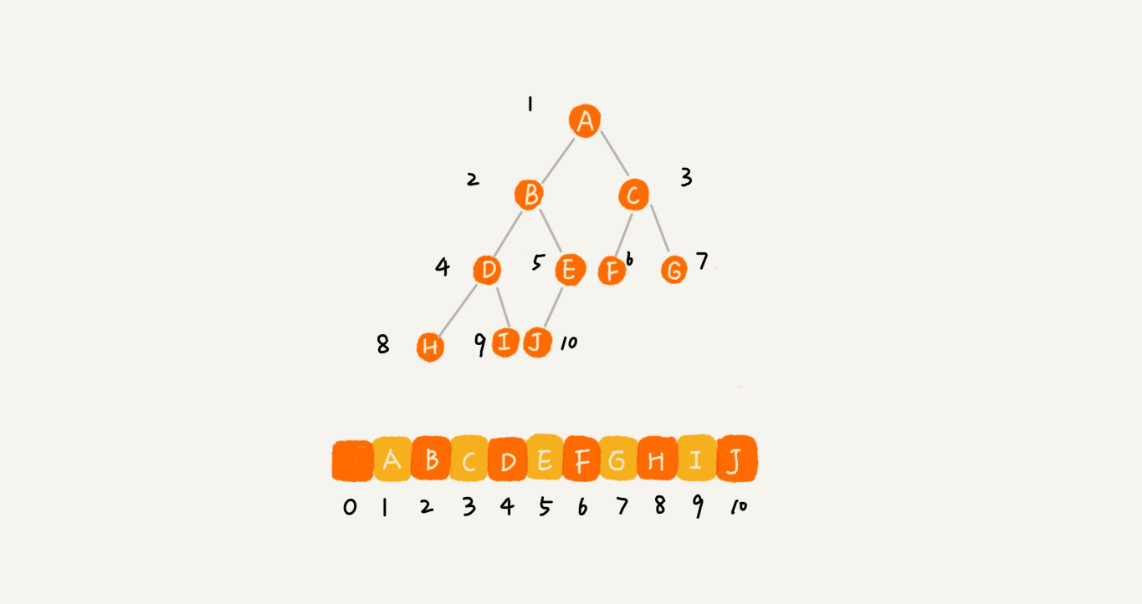
二叉树的遍历
- 前序遍历:对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。
- 中序遍历:对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树。
- 后序遍历:对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。
三种遍历的时间复杂度都为 O(n)。
二叉查找树
二叉查找树是二叉树中最常用的一种类型,支持动态数据集合的快速插入、删除、查找操作。其中序遍历即为顺序打印。
要求:在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值。
二叉查找树的查找操作
先取根节点,如果它等于我们要查找的数据,那就返回。如果要查找的数据比根节点的值小,那就在左子树中递归查找;如果要查找的数据比根节点的值大,那就在右子树中递归查找。
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15public Node find(Node root, int value) {
if (root == null) {
return null;
}
if (root.data == value) {
return root;
} else if (root.data > value) {
return find(root.left, value);
} else {
return find(root.right, value);
}
}
二叉查找树插入操作
新插入的数据一般都是在叶子节点上,所以只需要从根节点开始,依次比较要插入的数据和节点的大小关系。如果要插入的数据比节点的数据大,并且节点的右子树为空,就将新数据直接插到右子节点的位置;如果不为空,就再递归遍历右子树,查找插入位置。同理,如果要插入的数据比节点数值小,并且节点的左子树为空,就将新数据插入到左子节点的位置;如果不为空,就再递归遍历左子树,查找插入位置。
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21public void insert(Node root, Node newNode) {
if (root == null) {
root = newNode;
}
if (root.data < newNode.data) {
if (root.right == null) {
root.right = newNode;
} else {
insert(root.right, newNode);
}
}
if (root.data > newNode.data) {
if (root.left == null) {
root.left = newNode;
} else {
insert(root.left, newNode);
}
}
}
二叉查找树删除操作
删除操作针对要删除节点的子节点个数的不同,需要分三种情况来处理。
- 第一种情况是,如果要删除的节点没有子节点,只需要直接将父节点中,指向要删除节点的指针置为 null。
- 第二种情况是,如果要删除的节点只有一个子节点(只有左子节点或者右子节点),只需要更新父节点中,指向要删除节点的指针,让它指向要删除节点的子节点就可以了。
- 第三种情况是,如果要删除的节点有两个子节点,这就比较复杂了。需要找到这个节点的右子树中的最小节点,把它替换到要删除的节点上。然后再删除掉这个最小节点,因为最小节点肯定没有左子节点(如果有左子结点,那就不是最小节点了),所以,可以应用上面两条规则来删除这个最小节点。
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56public void delete(Node root, Node removeNode) {
if (root == null || removeNode == null) {
return;
}
Node temp = root;
Node parentNode = null;
while (temp != null && temp.data != removeNode.data) {
parentNode = temp;
if (temp.data > removeNode.data) {
temp = temp.left;
} else {
temp = temp.right;
}
}
// 没有找到要删除的,直接返回
if (temp == null) {
return;
}
// 删除的节点有两个节点
if (temp.left != null && temp.right != null) {
Node minNode = temp.right;
Node minNodeParent = temp;
while (minNode.left != null) {
minNodeParent = minNode;
minNode = minNode.left;
}
temp.data = minNode.data;
temp = minNode;
parentNode = minNodeParent;
}
// 删除叶子节点或只有一个叶子节点的
Node child;
if (temp.left != null) {
child = temp.left;
} else if (temp.right != null) {
child = temp.right;
} else {
child = null;
}
if (parentNode == null) {
root = child;
} else if (parentNode.left == temp) {
parentNode.left = child;
} else {
parentNode.right = child;
}
}
时间复杂度
- 最坏情况时间复杂度:最坏情况下二叉树左右节点极度不平衡,退化为链表,所以时间复杂度就变成了 O(n)。
- 最好情况时间复杂度:最好情况二叉树是一棵二叉树(或满二叉树)。时间复杂度跟树的高度成正比,即 O(height)。设最大高度为 h,节点个数为 n,则 n 和 h 满足 n = 1 + 2 + 4 + …… + 2h - 1 + 2 h。借助等比数列求和公式,可以计算出 h = log2n。可知最好情况时间复杂度为 O(logn)。
红黑树
二叉查找树在频繁的动态更新过程中,可能会出现的高度远大于 log2n的情况,导致各个操作的效率下降,极端情况下,二叉树会退化为链表,时间复杂度退化到 O(n)。要解决这个复杂度退化的问题,就需要设计一种平衡二叉查找树。红黑树是最常见的平衡二叉查找树。
平衡二叉查找树严格定义:二叉树中任意一个节点的左右子树的高度相差不能大于 1。AVL 树是最先被发明,且严格符合平衡二叉查找树定义的平衡二叉查找树。
很多的平衡二叉查找树其实并没有严格符合上述定义,只是让整棵树看起来相对的平衡,不要出现左子树很高、右子树很矮的情况。红黑树就是其中的一种。
红黑树需满足的几点要求:
- 每个节点不是红色就是黑色。
- 根节点是黑色的。
- 每个叶子节点都是黑色的空节点(NIL)。
- 如果一个节点是红色的,则他的两个子节点都是黑色的。
- 每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点。
红黑树示意图:
下图中黑色的、空的叶子节点已省略。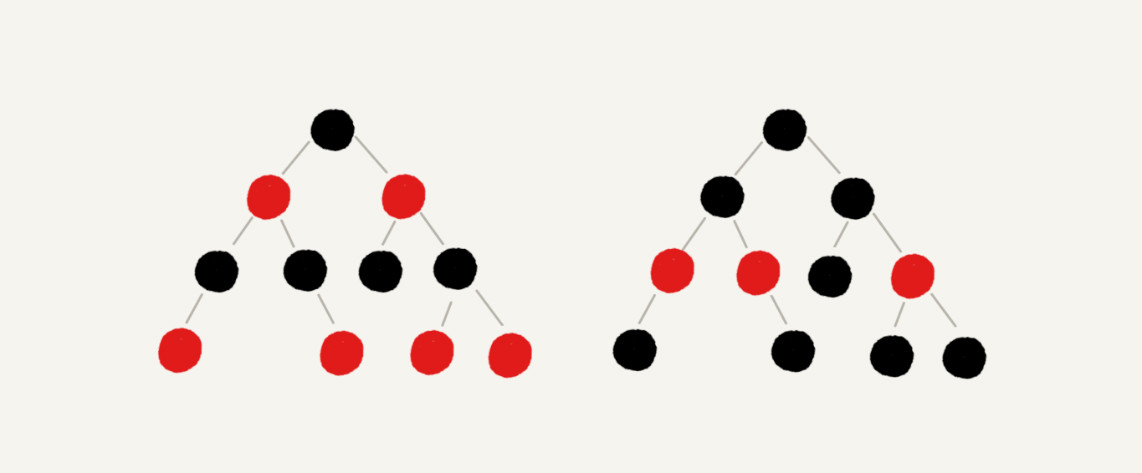
在红黑树的插入、删除节点的过程中,可能会破坏上述几点要求,就需要进行平衡调整,使其满足上述要求。调整的方法涉及左旋、右旋和改变颜色。
比较:AVL 树是一种高度平衡的二叉树,所以查找的效率非常高,但是,有利就有弊,AVL 树为了维持这种高度的平衡,就要付出更多的代价。每次插入、删除都要做调整,就比较复杂、耗时。所以,对于有频繁的插入、删除操作的数据集合,使用 AVL 树的代价就有点高了。红黑树只是做到了近似平衡,并不是严格的平衡,所以在维护平衡的成本上,要比 AVL 树要低。所以,红黑树的插入、删除、查找各种操作性能都比较稳定。对于工程应用来说,要面对各种异常情况,为了支撑这种工业级的应用,因此更倾向于这种性能稳定的平衡二叉查找树。
注:以上关于红黑树做简单介绍,了解更多信息内容可自行搜索。
跳表、散列表和平衡树的比较
- 跳表和各种平衡树(如AVL、红黑树等)的元素是有序排列的,散列表是无序的。因此,跳表和平衡树可以做范围查找,散列表只能做单个 key 的查找,不适宜做范围查找。
- 在做范围查找时,平衡树比跳表要复杂。在平衡树上找到指定范围的最小值后,还需以中序遍历的顺序继续查找其他不超过大值的节点。而在跳表上进行范围查找就比较简单,只需要找到小值后,对原始链表进行遍历查找即可。
- 平衡树的插入和删除操作可能会引发子树的调整,逻辑复杂,而跳表的插入和删除操作只需要修改相邻节点的指针,操作简单快速。
- 查找单个 key,跳表和平衡树的时间复杂度都为 O(logn),大体相当;而哈希表在保持较低的哈希值冲突概率的前提下,查找时间复杂度接近 O(1),性能更高一些。
- 从算法实现难度上来比较,跳表比平衡树要简单得多。